安定极限常常被用于表征弹塑性结构的极限承载能力。当循环载荷水平高于弹性极限(Elastic limit, EL)、但低于结构安定极限(Elastic shakedown limit, ESL)时,弹塑性结构在若干初始的加载周次内出现有限的塑性变形后,便会达到稳定的弹性响应状态,不再发生新的塑性流动;在高于安定极限的循环载荷作用下,弹塑性结构最终会因交变塑性或棘轮破坏而发生失效。因此,开展功能梯度涂层/基体结构的安定分析并评估相应的接触安定极限,对于功能梯度涂层的参数优化以及在接触领域内的工业化应用具有重要意义。然而,目前功能梯度结构的安定分析主要集中于Bree板、圆盘和空心球等结构,而针对功能梯度涂层/基体结构的接触安定研究还比较匮乏。鉴于此,新葡萄88805官网康国政教授课题组基于静力安定理论,构建了功能梯度涂层/基体结构的热弹性滚动/滑动接触安定计算模型,绘制了功能梯度涂层/基体结构的安定图。
考虑如图1所示的接触问题,其中两个圆柱的物性参数相同,均含有相同厚度的功能梯度表面涂层,涂层内的剪切模量、屈服应力、热导率、热扩散率和热膨胀系数可沿厚度方向呈任意梯度变化。同时,假设接触过程中因摩擦做功而损失的机械能全部转化为热能,并以热传导的方式平均传递给两个圆柱内部;忽略圆柱间的相互导热作用,而接触区域之外的表面与周围环境间也不发生热交换。为了处理涂层内部物性参数的梯度分布,将功能梯度涂层近似成由均匀层组成的叠层结构(见图2)。

图1接触示意图:P和Q分别表示法向和切向载荷,R1和R2分别表示上下圆柱的半径,h、V和Ω分别表示功能梯度涂层厚度、上圆柱的滚动速率以及角速率;p和q分别表示接触斑内的法向接触压力和表面切应力
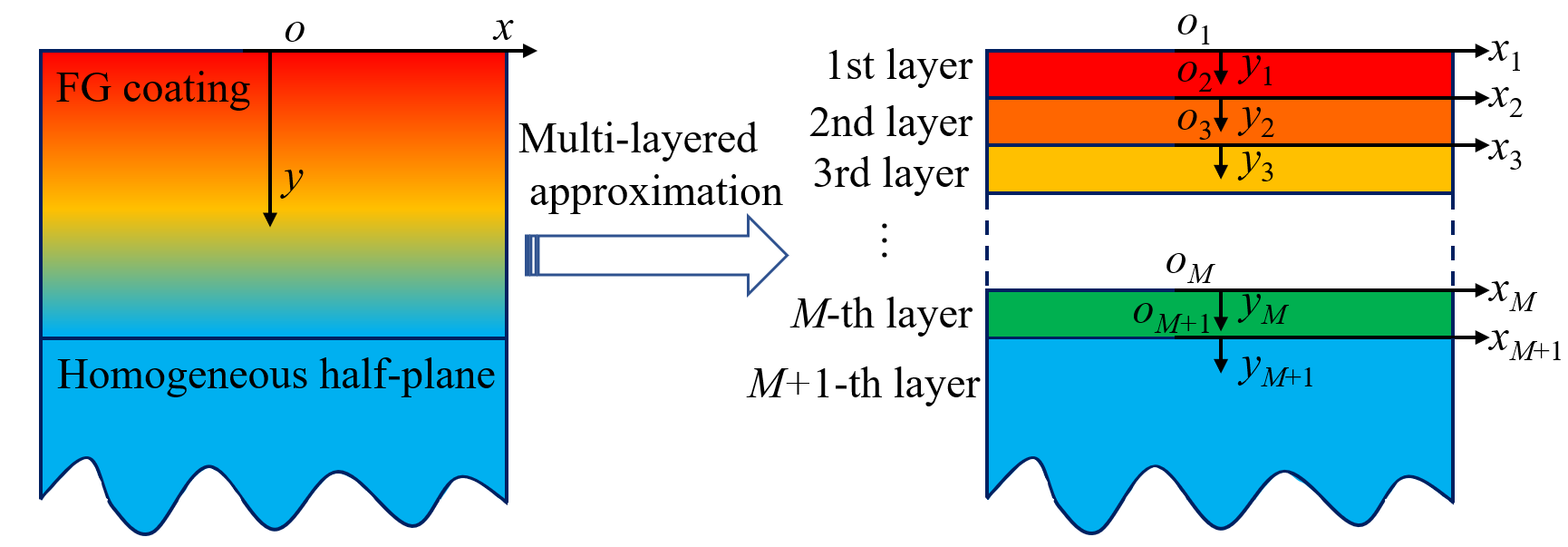
图2功能梯度结构的叠层近似示意图
基于傅里叶变换和传递矩阵法,利用均匀层的弹性通解形式和相邻层间温度、温度梯度、位移以及应力的连续条件,并结合边界条件,获得了热弹性位移和应力在频域内的通解;接着,利用离散卷积-快速傅里叶变换(Discrete convolution-fast Fourier transform, DC-FFT)算法和共轭梯度法(Conjugate gradient method, CGM)对热弹性接触应力分布进行了求解。其中,共轭梯度法通过不断更新表面变形,来驱动表面接触压力的迭代过程,直至表面接触压力趋于收敛;离散卷积-快速傅里叶变换算法则用于提高表面接触应力与弹性场间的映射计算的效率。最后,结合获得的接触应力结果,基于静力安定理论和Tresca屈服准则,构建了功能梯度涂层/基体结构的二维热弹性滚动/滑动接触安定计算模型,讨论了摩擦系数、滚动速率以及物性参数梯度分布形式等参数对安定极限曲线的影响。研究结果为功能梯度涂层工艺参数的进一步优化提供支撑。
该研究论文以Elastic shakedown analysis of two-dimensional thermo-elastic rolling/sliding contact for a functionally graded coating/substrate structure with arbitrarily varying thermo-elastic properties为题发表在Composite Structures上。博士研究生伏培林为论文第一作者,赵吉中、张旭、康国政和土木工程学院王平教授为共同作者,阚前华教授为本文的通讯作者。课题组长期致力于开发复杂条件下的材料循环塑性本构模型,结合数值分析开展结构的疲劳失效寿命预测,为结构关键零部件的损伤演化和寿命评估提供指导。
原文链接:https://doi.org/10.1016/j.compstruct.2021.114891



